概述
卷积是一种线性运算,实在质是滑动均匀思想,广泛运用于图像滤波。而随着人工智能及深度学习的发展,卷积也在神经网络中发挥主要的浸染,如卷积神经网络。本参考设计紧张先容如何基于INTEL 硬浮点的DSP Block实现32位单精度浮点的卷积运算,而针对定点及低精度的浮点运算,则须要对硬浮点DSP Block进行相应的更换即可。

事理剖析
设:f(x), g(x)是两个可积函数,作积分:
随着x的不同取值,该积分定义了一个新的函数h(x),称为函数f(x)与g(x)的卷积,记为h(x)=f(x)g(x)。
如果卷积的变量是序列x(n)和h(n),则卷积的结果为
个中表示卷积。因此两个序列的卷积,实际上便是多项式的乘法,用个例子解释其事情事理。a = [7,5,4]; b = [6,7,9];则实现a和b的卷积,便是把a和b作为一个多项式的系数,按多项式的升幂或降幂排列,即为:
因此得到ab=[42,79,122,73,36];与Matlab运算结果同等。而二维卷积可以采取通用多项式乘积方法实现卷积运算。
基于INTEL FPGA的实现剖析
如上我们确定了两个序列的卷积等同于两个多项式的乘法,因此当我们须要打算序列[a0,a1,a2, …,an-1]与[b0,b1,b2, …,bn-1]的卷积结果时,可以成立a,b两个n阶多项式,如下所示:
则[a0,a1,a2, …,an-1]与[b0,b1,b2, …,bn-1]的卷积结果即为由ab得到的多项式的各项系数所组成的序列。令c=ab,得到
则由多项式c的各阶系数所组成的新的序列[c0,c1,c2, …,c2n-1]即为[a0,a1,a2, …,an-1]与[b0,b1,b2, …,bn-1]的卷积结果。则按照高阶多项式打算展开可得到:
┆┆
┆┆
因此卷积的运算可以转化为行向量与列向量相乘的结果,即乘累加的运算构造。
Intel FPGA在Arria10DSP Block中首次支持了单精度硬浮点DSP block,是行业内第一个支持单精度DSP block,硬浮点DSP block架构如图1所示:
图1 硬浮点DSPblock架构
硬浮点DSP Block包含硬浮点乘法器,硬浮点加法器,支持乘累加运算,因此采取硬浮点DSPblock实现行列向量相乘是非常好的办法。下面我们针对一个实际的卷积运算,先容如何基于INTEL硬浮点DSP block实现。假设我们须要求随机数组a=[4,8,9,11]与b=[10,5,7,13]的卷积运算结果,则根据上面的剖析,保持数组a顺序不变,而数组b需根据上述剖析结果,针对每一个卷积结果产生新的序列。以是全体实现包括数列重组模块和硬浮点乘法器模块及输出处理。下面是实现框图及仿真结果。
图2 实现框图
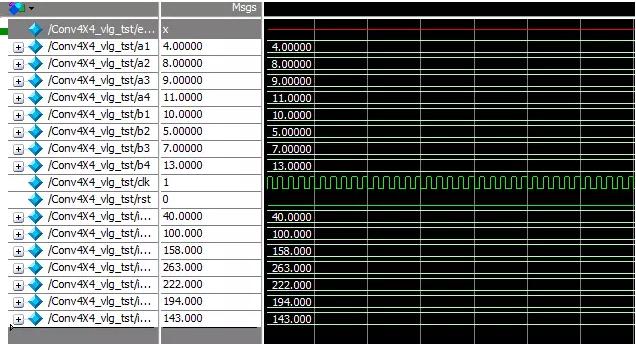
图3 Modelsim仿真结果
仿真结果与Matlab实现结果同等,并且该设计中充分考虑了FPGA并行扩展特性,对付低速率哀求的设计可采取DSP Block复用的办法节约DSP block数量。
版权所有权归卿萃科技,转载请注明出处
作者:卿萃科技ALIFPGA
原文地址:卿萃科技FPGA极客空间 微信"大众号
















