「Coding Master」第4话 运用基本逻辑门、加法器搭建ALU_全加器_加法

通过基本逻辑门可以搭建更繁芜的电路，比如异或门，异或门用了四个基本逻辑门。
只有在两个输入不一样时，输出才为1。
本期我们将利用这些逻辑门，搭建更繁芜的加法减法等电路实现。

在这里我们引入一个抽象的观点，比如异或门利用了四个基本逻辑门。
我们在后续的电路设计中，会直策应用异或门，不再把每个基本逻辑门，或者每个晶体管画出来。
基本逻辑门是晶体管的抽象，异或门便是那四个基本逻辑门的抽象。
我们把它看作一个元件来利用，并且明了它的逻辑功能，利用其他逻辑门时同理。

打算机是如何做加法呢？我们先来看最大略的2个1位的二进制数相加，可以看出，加法最大结果是10。
也便是2个1位数相加最多须要2位来保存结果，1位保存和，1位保存进位。

我们来看看进位还有和的值，不丢脸出，进位的值跟X、Y“与”运算结果一毛一样。

而和的值跟X、Y“异或”运算的结果保持同等。

这么说，我们可以用一个与门一个异或门，来搭建一个2位的加法器，详细的电路图便是这样了。
异或门来打算和，与门来打算进位。
X、Y都为0，则和与进位都为0；X=1，Y=0，则和为1，进位是0；X=0，Y=1，同样和为1，进位是0；X=1，Y=1，和为0，进位是1，这个电路称为半加器。

半加器有2个输入X、Y，2个输出，分别是和以及进位。
它能产生进位，但是不能处理进位。
这是另一层抽象，我们可以把半加器作为一个元件来利用。
我们再进一步，制造一个可以做3位加法的电路。

3个1位二进制数相加，最大值便是1+1+1=11，同样可以用2位保存结果。
详细电路实现，我们可以用2个半加器和1个或门来搭建。
一共有3个输入X、Y、Z，我们把X、Y输入到第一个半加器，输出的和跟Z一起输入到第二个半加器。
然后把两个半加器的进位输入到或门，第二个半加器输出的和便是终极的和，而或门的输出便是进位。

两个进位是不可能同时为1的，由于任意两个输入相加，如果产生了进位，那么和一定是0。
再加上一位无论是0还是1，都不会产生进位。

我们把3个1位数相加的所有情形都列出来，一共有8种。
然后再把电路拉出来，X、Y、Z是三个输入位，XOR 1跟AND 1组成了第一个半加器，XOR 2跟AND 2组成了第二个半加器，OR 1处理两个半加器的进位，这便是全加器的所有电路。

XOR 1的输出是X+Y的和，作为XOR 2还有AND 2的输入。
AND 1的输出是X+Y的进位，作为OR 1的输入。
Z是XOR 2的第2个输入，XOR 2的输出是终极的和。
同时，Z也是AND 2的输入。
AND 2的输出和AND 1的输出共同作为OR 1的输入，OR 1的输出便是终极的进位。

当X、Y、Z全部都是0，和与进位都是0；当X、Y、Z分别为1，和为1，进位是0；当X、Y、Z中有2个为1，另一个为0，则和为0，进位是1；当X、Y、Z全都是1的时候，和为1，进位也是1。
全加器可以吸收3个输入，并产生和以及进位，同时它也可以处理打算中产生的进位。
现在我们的武器库升级了，全加器是一个全新的抽象。

它接管3个输入，并输出和与进位，它也能处理打算过程中的进位。
有了半加器和全加器，我们又可以更上一层楼了。
打算机中1个1位的二进制数称为1个比特（Bit），也可以叫1位，而8个比特长度的二进制数称为1个字节（Byte）。

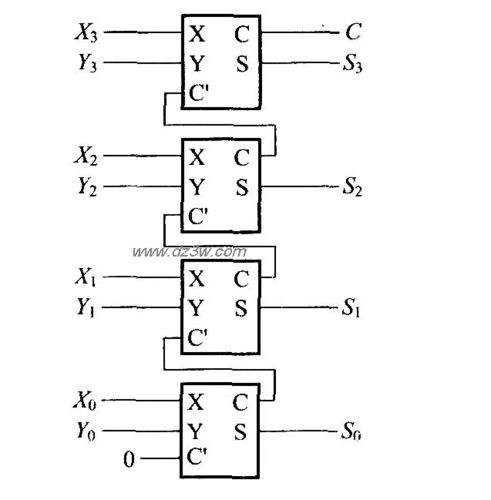
现在我们来搭建一个8位的打算单元，也便是可以接管2个单字节的数A、B作为输入，然后打算它们的和。
1个字节共有8个比特，即8位，而打算机中序号是从0开始的。
便是说，1个字节的第1位，序号是0。
而第8位，序号是7，这个序号我们称为索引（Index）。

A0+B0可以用一个半加器处理，由于不须要处理来自上次打算的进位。
而A1+B1须要处理A0+B0的进位以及A1、B1本身，以是须要1个全加器，来处理这3个输入。
从A1、B1到A7、B7，都须要处理进位，以是必须都用全加器处理。

我们用1个半加器和7个全加器，就制造了一个可以处理两个字节A、B加法的打算单元。
同时我们把稳到，末了一个全加器的进位是没有被处理的。
以是这可能会导致打算缺点，我们称之为溢出。

那么，它可以做减法吗？可以，但是跟我们平常做减法不一样。
打算机里的减法，也是通过加法来实现的，比如我们8-3等价于8+（-3）。
那么打算机是怎么表示负数的呢？大略起见，我们以一个4位的打算机为例。

4位的打算机，能处理的最大的数是1111。
我们从0000开始，每次加1，在加了15次之后，我们得到了1111。
那么1111+1即是多少呢？正常该当是10000，但是这是一个4位的打算机。
以是最高位的1是没法存储的，以是被丢弃了。
那么末了结果便是0000，这就又回到了最初的出发点。

就像钟表一样，指针转完一圈就开始新的一圈，我们也做一个4位二进制表盘。
从0000开始顺时针旋转，一贯到1111一共16个数字。
但是打算机只认识0和1，它可不知道正负数。
表盘的16个数字，我们以0000为分边界做个切分。
拿出一部分来表示负数，比如最高位是1的部分。
那么最高位就成了一个标志位，是0便是正数，是1就表示负数，0的二进制便是0000。

而0向右依次加1，就得到了正整数。
向左依次减1，就得到了负整数。
然后我们把这些数字铺下去，以0为基准，顺时针旋转1下，得到1，再转一下得到2，以此类推。
以0为基准，逆时针旋转一下，得到-1，再转一下得到-2，很合理吧。
而数学里是没有+0和-0之分的，以是1000不是表示-0，而是表示-8。

我们在这个表盘上做个减法，比如2-3，先把当前位置定到2，-3的话便是逆时针旋转3下，就来到了-1这里。
这个很大略，由于我们这个表盘是个循环，以是我们还有另一种方法到达-1。
便是从2的位置，连续顺时针旋转，13下之后就到了-1。

由于从2出发，转一整圈还会回到2，就犹如钟表一样。
以是2+16实在就等效于2，以是2-3也即是2+16-3，这里结合咱们的表盘，停下来想一想。

而对付-1～-7，如何打算它在表盘上的二进制数呢？我们以-1为例，+1的二进制数为0001。
那么我们先把标志位切换为1，得到1001，这个叫做-1的原码。
然后把1001除了标志位外的3位取反，得到1110，这个叫做-1的反码。
然后再把反码加1，得到1111，这便是-1的补码。

-1～-7在表盘上对应的二进制数字，便是补码。
0和正整数1～7的原码、反码、补码都是一样的。
-8有点不一样，1000本来是表示-0，但是只有1个0。
以是-8的原码、反码、补码都是一个码1000。
实在1000也即是+7的码0111+1。

这里我做了个表格，总结了4位打算机下的整数表示。
范围是-8～7，共计16个数字。
同时，这个理论也适用于任何多位的打算机，无论是8位、32位、64位，方法都一样。

那我们来做个减法 7-3，首先我们获取-3的原码1011，然后取反得到-3的反码1100，在把反码+1得到-3的补码1101。
7的补码是0111，0111+1101=10100，最高位的1会被丢弃，以是末了结果是0100，也便是4。

这里做一个把4位机拓展到N位机的小总结，我就不念了，各位同学自己看看。

那我们那个8位的打算单元，能做乘除法吗？必须的，只不过乘法是通过拆成加法来做的，比如4x5，便是4个5相加。
而除法是先拆成减法，比如20/5，便是20持续的减5，再把减法通过加法实现。

总而言之，这个8位打算单元，加减乘除都能做。
而更前辈的CPU，可以通过搭建专业的电路来做乘除法，这里我们不再深入。

同时，打算机除了做打算之外，还须要做一些逻辑判断。
比如判断打算结果是否溢出，这个我们在全加器那提到过。
判断结果是否为0，可以额外搭建一个电路。
判断奇偶性则可以通过判断终极结果的最低位是否为0。
我们来看看判0电路怎么做，8位的打算单元输出是8位，我们用7个或门，依次打算个中任意一位是否为1，就可以得出结论了。

而打算单元+逻辑单元，组合起来就得到了一个ALU。
全称是逻辑运算单元，既能做逻辑判断也能做加减乘除等打算，我们用一个大V来表示。
它接管2个8位也便是1字节的输入，同时输出1个8位的结果。
它接管1个4位的操作码，比如1000代表加。
也会输出诸如结果是否为0或者为负值等逻辑状态，这便是一个基本全功能的ALU了。

而诸如我们提到的1000代表加法，这便是打算机指令。
天下上第一个封装到单芯片中的完全ALU，是英特尔的74181芯片，它利用了70个晶体管，是一个4位的ALU。

好了，本期视频就到这里，是不是觉得脑细胞不太够用？没紧要，下节课讲寄存器啊内存什么的，比较好理解。
下期见！