浅谈“数字电路”的进修（5）—被教程忽视的加法器_加法器_全加器

虽然我们对十进制的加减乘除都已经熟习到了本能的地步，如何让晶体管构建的、以二进制为根本的数字电路来实现我们人类须要的加、减、乘、除？

准确地讲便是在我们的数字电路中一带而过的Adder - 半加器、全加器以及超提高位加法器（很多教程仅给出了半页的篇幅）。
冬瓜哥得出的结论是“CPU内部便是个加法器”。
可见它的主要性，也可见我们对它真的是严重忽略了，就像1+1=2一样，它主要得实在太平凡了。

但，它确实是我们数字打算的根本，理解了它才能够理解全体的数字逻辑天下。

我们先通过硬禾学堂制作的一个7分钟的视频教程来看一下加法器最基本的两个示例：

视频加载中...

第一个案例 - 1位半加器

根据我们人类在十进制领域定义的加法规则，来操作2个1位的数据相加，从最基本的门的功能以及加法的规则需求，我们得到来实现它的电路 - 通过一个“异或门”得到加法往后的1位的结果，以及通过一个“与门”得到一个“进位”位的值，就像我们十进制的加法，如果两个数字相加超过了一个“位”（十进制的位）能够表达的范围，就要天生一个进位旗子暗记。
通过真值表能够比较直不雅观地看出反响2个输入位同经由加法操作往后得到的输出位的关系。

利用Verilog代码的1位半加器：

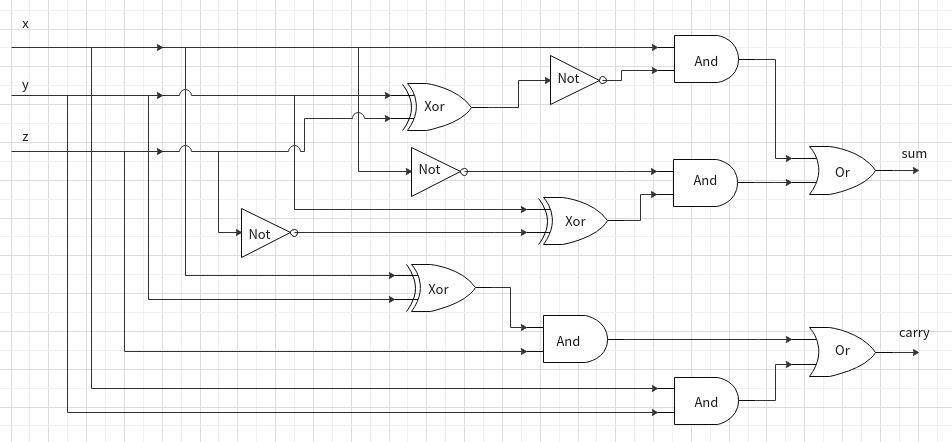
第二个案例 - 1位全加器

毕竟2个1位的数相加只是根本，太局限，我们扩展一下，如果须要有超过1位的数字相加，该如何操作？那就须要将“进位”的值考虑进来，作为一个输入，有了进位输入、进位输出的加法器被称之为“全加器”，全了，谁都不缺了。

利用Verilog代码的1位全加器的Verilog代码：

通过上面的两段Verilog代码，可以看出用Verilog这种硬件描述措辞的一些特点，这个在后面的文章中会专门先容。

多数的“数字电路”教程关于加法器也基本上点到此为止了。

但上述的基本单元能用来做啥的？如果不做扩展，同学们很难有进一步的理解，因此我建议大家可以自行做一些扩展：

支持多位二进制数相加的并行二进制加法器

比如2个4位二进制的加法器，它可以由3个全加器和1个半加器构成，低位的加法进位可以作为相邻高位加法的一个输入端，最低位仅用一个半加器，最高位天生的进位旗子暗记作为后续电路的输入。

是不是像极了我们的十进制加法？事理是一样的，只是采取的进制不同，而二进制可以通过数字电路的0、1比较随意马虎地实现。

理解了加法器，减法器也就不难明得，就像我们十进制中的加和减的关系一样。
它的基本规则：

对应的也有：

1位半减器

一位半减器的符号、电路构成以及真值表

1位全减器

用半减器构成的全减器

并行二进制减法

用三个全减器和一个半减器构成的4位并行减法器

用4个全加器也可以构成一个4位并行减法器

既然多位的全减器也可以用全加器来实现，是不是可以有一种统一的构造能够实现加、减的功能？毕竟减和加是对偶的，减法也可以看作是+（-）的操作。

统一构造的并行加、减法

从前面的加减法构成可以看出，加法器和减法器都可以用共同的加法器来实现，如果我们添加一个掌握旗子暗记M，最低位也利用一个全加器，将这个M值连接到该全加器的进位输入端，就可以通过这个M是0或1来决定此电路时加法电路还是减法电路：

如果你须要将更多的位数的二进制数字相加或相减，你可以利用更多个加法器级联即可得到。
细心和动脑的同学会创造，如果任何操作须要哪怕一丁点的韶光（有了韶光的观点也就意味着 - 因果之间有了先后，有了“时延”，我们生存的天下韶光是一个客不雅观存在的维度），那么图中的操作在每个位上的输出就会产生韶光上的差异，最高位的值和进位依赖于低位的值和每一位加法操作的韶光（也便是构成加法器的门的相应韶光）。
就像绿灯亮起，并不是所有等待的车同时启动前行，而是从第一辆车逐级通报过来的一样。

用上述方法构建的加法器、减法器，位数越多，由于电路门时延带来的打算结果会越慢涌现，聪明的前辈大神们竟然通过一系列的逻辑运算发明了“超提高位加法器”的构造，即便实际的电路上每个操作都有先后带来的时延，我们也可以不须要考虑每个进位的逐级通报，而是一次性地根据各个输入真个位上的值直接得出运算往后的结果。

是不是很不可思议？

为啥须要逐级通报的信息可以提前预知？为什么在布尔表达式中的一些变量经由逻辑化简往后创造它们只是打酱油的可有可无？

我们的生活中是否也是如此？每当绿灯亮起的时候所有的车是否也能同步启动前行？

这些问题留给大家思考。

有了加法器、减法器，也就很随意马虎构建乘法器 - 重复多次的加，和除法器 - 重复多次的减。

因此加法器是构成全体数字打算的根本，是最主要的一个部件，它的设计好坏直接影响了处理器/掌握器的性能、性价比等。

比如在电子森林“电路仿真”中的Brent-Kung树形加法器便是一种最小化芯片面积和本钱的构造。
有兴趣的同学可以点击https://www.eetree.cn/war/circuitjs.html?lang=zh 来体验一下。

正如前面文章所述，在FPGA没有大面积遍及运用的年代，曾经有一系列的中等规模的集成电路模块推出，最著名的便是74系列的器件，个中74HC283便是一种4位超提高位的全加器器件。
很多高校可能还在拿它做数电的实验。

形状长这样

内部功能这样

末了，给大家先容一款国外公司制作的4位加法器的演习套件。

我们平时在面包板上做是这样的

这个公司画成了电路板，就卖55美元了 - 想不想学习一下自己设计PCB？也是很主要的一个技能。

功能框图

为了方便大家实验，这个产品中包含了如下的一些器件：

得说，这个套件的文档写得特殊的棒，有兴趣的老师和同学可以自己搜一下。

这个套件用了8颗中等规模的集成电路，加上很多连线连线。
实在呢，用小脚丫FPGA内部的不到1%的资源就能实现，而且只须要写很短的几行Verilog代码。

要不您试一下？

前期与数电干系的文章：